Pooling Layer

Pooling

Pooling은 sub sampling이라고 함 

image data를 작은size의 image로 줄이는 과정

pooling을 사용하는 이유
앞선 layer들을 거친 output의 모든 data가 필요하지 않기 때문
→ 즉, 추론을 하는데 있어 적당량의 data만 있어도 되기 때문

pooling의 특징 

1. 학습변수가 없다. (ex. weight, bias)
2. pooling의 output은 channel수에 영향 없다.

Max Pooling

최댓값을 뽑아내는 pooling의 한 종류

$\phi =\max \left( W\right) $

1D Max Pooling

import numpy as np
import tensorflow as tf
 
from tensorflow.keras.layers import MaxPooling1D
 
L, f, s = 10, 2, 1
 
# input , shape= datasample의 갯수, length, channel
x = tf.random.normal(shape=(1, L, 1))
pool_max = MaxPooling1D(pool_size = f, strides = s)
pooled_max = pool_max(x)
 
print("x: {}\n{}".format(x.shape, x.numpy().flatten()))
print("pooled_max(Tensorflow): {}\n{}".format(pooled_max.shape, pooled_max.numpy().flatten()))
 
x = x.numpy().flatten()
pooled_max_man = np.zeros((L -f + 1, ))
for i in range(L -f +1):
  window = x[i:i+f]
  pooled_max_man[i] = np.max(window)
 
print("pooled_max(Manual: {}\n{}".format(pooled_max_man.shape, pooled_max_man))

2D Max Pooling

import numpy as np
import tensorflow as tf
 
from tensorflow.keras.layers import MaxPooling2D
 
N, n_H, n_W, n_C = 1, 5, 5, 1
f, s = 2, 1
 
x = tf.random.normal(shape=(N, n_H, n_W, n_C))
# pool =  f by f
pool_max = MaxPooling2D(pool_size=f, strides = s)
pooled_max = pool_max(x)
 
print("x: {}\n{}".format(x.shape, x.numpy().squeeze()))
print("pooled_max(Tensorflow): {}\n{}".format(pooled_max.shape, pooled_max.numpy().squeeze()))
 
x = x.numpy().squeeze()
pooled_max_man = np.zeros(shape=(n_H - f + 1, n_W - f + 1))
for i in range(n_H - f + 1):
  for j in range(n_W - f + 1):
    window = x[i:i+f, j:j+f]
    pooled_max_man[i, j] = np.max(window)
 
# output shape = (n_H-f+1, n_W-f+1)
 
print("pooled_max(Manual): {}\n{}".format(pooled_max_man.shape, pooled_max_man))

3D Max Pooling

#multi channel input
import math # gauss func
import numpy as np
import tensorflow as tf
 
from tensorflow.keras.layers import MaxPooling2D
 
N, n_H, n_W, n_C = 1, 5, 5, 3
f, s = 2,2
 
x = tf.random.normal(shape=(N, n_H, n_W, n_C))
#channel wise로 보기위해 transpose
# x.numpy().squeeze = (5, 5, 3)
# np.transpose(x.numpy().squeeze(), (2,0,1)) = (3, 5, 5)
print("x: {}\n{}".format(x.shape, np.transpose(x.numpy().squeeze(), (2,0,1))))
pool_max = MaxPooling2D(pool_size = f, strides = s)
pooled_max = pool_max(x)
 
pooled_max_t = np.transpose(pooled_max.numpy().squeeze(),(2,0,1))
print("pooled_max(Tensorflow): {}\n{}".format(pooled_max.shape,pooled_max_t))
 
x = x.numpy().squeeze()
n_H_ = math.floor((n_H - f)/s + 1)
n_W_ = math.floor((n_W - f)/s + 1)
pooled_max_man = np.zeros(shape=(n_H_,n_W_,n_C))
 
# channel별로 들어옴
for c in range(n_C):
  c_image = x[:, :, c]
 
# input image의 index와 output image의 index가 달라 변수설정
  h_ = 0
  for h in range(0, n_H - f + 1, s):
    w_ = 0
    for w in range(0, n_W - f + 1, s):
      window = c_image[h:h+f, w:w+f]
      pooled_max_man[h_, w_, c] = np.max(window)
 
      w_ += 1
    h_ += 1 
 
pooled_max_t = np.transpose(pooled_max_man,(2,0,1))
print("pooled_max(Manual): {}\n{}".format(pooled_max_man.shape,pooled_max_t))

results
x: (1, 5, 5, 3)
[[[-0.04165245 -0.69489294 0.2628172 -1.4416945 0.32234243]
[-0.79485124 -1.2013087 -1.2264383 0.8739131 -0.7393973 ]
[-0.8175927 -0.32816795 -0.712461 -1.6772014 -0.36527568]
[-1.825489 1.2413286 0.14806442 -2.4312792 -0.9400049 ]
[-0.5953234 -0.6701633 1.246382 0.0760054 -0.66434175]]
[[ 0.69569916 -0.4265282 1.0689193 -2.368038 -2.049476 ]
[ 0.3202273 -0.09945048 0.10267391 1.9018568 -0.40930164]
[-0.332641 0.9687359 -0.5321431 1.397498 -2.3049204 ]
[-0.8621706 -0.30300015 -0.02255699 -0.5857848 0.8662503 ]
[ 0.01320763 -1.2768902 1.6485813 0.7326172 -0.6582798 ]]
[[-0.44493952 0.9499523 -0.9830161 0.78371817 -0.88013387]
[ 0.5741747 -0.5608523 0.11236259 0.20844218 -1.5184106 ]
[ 0.05717982 -0.05508999 0.00551856 0.48005813 -0.87953824]
[-1.1947052 0.86224306 0.17340192 -0.6662103 2.0635462 ]
[-1.9396527 0.80733216 -0.391985 -0.8547198 -2.0354655 ]]]
pooled_max(Tensorflow): (1, 2, 2, 3)
[[[-0.04165245 0.8739131 ] [ 1.2413286 0.14806442]]
[[ 0.69569916 1.9018568 ] [ 0.9687359 1.397498 ]]
[[ 0.9499523 0.78371817] [ 0.86224306 0.48005813]]]
pooled_max(Manual): (2, 2, 3)
[[[-0.04165245 0.87391311] [ 1.2413286 0.14806442]]
[[ 0.69569916 1.90185678] [ 0.96873587 1.39749801]]
[[ 0.9499523 0.78371817] [ 0.86224306 0.48005813]]]

Average Pooling

평균값을 뽑아내는 pooling의 한 종류

$\phi =\dfrac{1}{\left\| W\right\| }\sum _{x\in W}x$

1D Average Pooling

import numpy as np
import tensorflow as tf
 
from tensorflow.keras.layers import AveragePooling1D
 
L, f, s = 10, 2, 1
 
# input , shape= datasample의 갯수, length, channel
x = tf.random.normal(shape=(1, L, 1))
pool_avg = AveragePooling1D(pool_size = f, strides = s)
pooled_avg = pool_avg(x)
 
print("x: {}\n{}".format(x.shape, x.numpy().flatten()))
print("pooled_avg(Tensorflow): {}\n{}".format(pooled_avg.shape, pooled_avg.numpy().flatten()))
 
x = x.numpy().flatten()
pooled_avg_man = np.zeros((L -f + 1, ))
for i in range(L -f +1):
  window = x[i:i+f]
  pooled_avg_man [i] = np.mean(window)
 
print("pooled_max(Manual: {}\n{}".format(pooled_avg_man .shape, pooled_avg_man))

2D Average Pooling

import numpy as np
import tensorflow as tf
 
from tensorflow.keras.layers import AveragePooling2D
 
N, n_H, n_W, n_C = 1, 5, 5, 1
f, s = 2, 1
 
x = tf.random.normal(shape=(N, n_H, n_W, n_C))
# pool =  2 by 2
pool_avg = AveragePooling2D(pool_size=f, strides = s)
pooled_avg = pool_avg(x)
 
print("x: {}\n{}".format(x.shape, x.numpy().squeeze()))
print("pooled_avg(Tensorflow): {}\n{}".format(pooled_avg.shape, pooled_avg.numpy().squeeze()))
 
x = x.numpy().squeeze()
pooled_avg_man = np.zeros(shape=(n_H - f + 1, n_W - f + 1))
for i in range(n_H - f + 1):
  for j in range(n_W - f + 1):
    window = x[i:i+f, j:j+f]
    pooled_avg_man[i, j] = np.mean(window)
 
# output shape = (n_H-f+1, n_W-f+1)
 
print("pooled_max(Manual): {}\n{}".format(pooled_avg_man.shape, pooled_avg_man))

 

Conv와 Pooling

공통점

1.  window를 뽑아냄
2. scalar값 1개 만듬

차이점

Conv의 경우, 

Layer안에 convolution연산과 activation func.을 지남

Pooling의 경우,

max pooling→ max값, average pooling → average값 뽑는게 끝

 

 

Padding

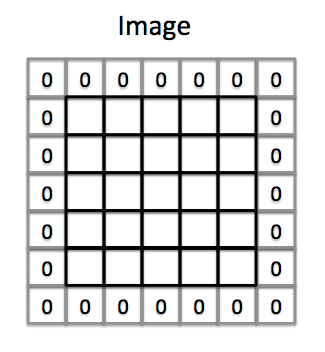
input 주변에 어떤 값들을 채워주는 것 

convolution 연산 시 corner pixel들을 잃어버림

→ 여러개의 conv layer를 거치면 pixel손실이 커짐, 방지하기 위해 image크기를 늘려줌

Padding의 효과
1. convolution 연산시,
input의 corner pixel이 몇번 수행되지 않는 것을 방지해줌
→ 모든 pixel이 동등하게 연산 되도록
2. input size와 output size의 shape이 같다 ((f-1)/2 = p 일 경우)

$n_{H}^{'}= n_{H}+2p-f+1 $ 

Zero Padding 2D Layer

import tensorflow as tf
 
from tensorflow.keras.layers import ZeroPadding2D
 
images = tf.random.normal(shape=(1, 28, 28, 3))
print(images.shape)
# print(np.transpose(images.numpy().squeeze(), (2, 0, 1)))
 
zero_padding = ZeroPadding2D(padding=1)
y = zero_padding(images)
 
print(y.shape)
# print(np.transpose(y.numpy().squeeze(),(2, 0, 1)))

Zero Padding with Conv2D Layer

import tensorflow as tf
 
from tensorflow.keras.layers import Conv2D
 
images = tf.random.normal(shape=(1, 28, 28, 3))
# padding = 'vaild' or 'same'
# same은  input shape = output shape 하도록 padding을 해줌 -> (f-1)/2 = padding size
conv = Conv2D(filters = 1, kernel_size = 3, padding='same')
y = conv(images)
print(y.shape)

Strides

window slicing을 띄엄띄엄 하는 것

stride가 필요한 이유
계산 효율성이나 다운 샘플링을 원하기 때문
기본 이미지의 넓은 영역을 캡처하기에 컨볼루션 커널이 클 때 유용
→ 출력의 해산도를 줄여줌

$W_{i,j}=X\left[ i:i+\left( f-1\right) ,j:j+\left( f-1\right) \right] $

$0\leq i\leq n_{H}-f,i=i^{'}\cdot S,i^{'}\in \mathbb{W} $
$0\leq j\leq n_{H}-f,j=j^{'}\cdot S,j^{'}\in \mathbb{W} $
ex) s = 2 → $i^{'}=0,1,2\ldots$ , $i = 0,2,4\ldots$와 같은 index가 만들어짐

$n_{H}^{'}=\left[ \dfrac{n_{H}-f}{s}+1\right] $ → 중간 끊킴 때문에 가우스 함수 도입

Strides in Conv2D Layers

import tensorflow as tf
 
from tensorflow.keras.layers import Conv2D
 
images = tf.random.normal(shape=(1, 28, 28, 3))
# valid = no padding
conv = Conv2D(filters=1, kernel_size = 3, padding='valid',strides=2)
y = conv(images)
 
# n_H_ = [(n_H + 2p - f)/s + 1]
print(images.shape)
print(y.shape)
 
# conv layer는 filter의 갯수에 따라 channel의 수가 정해짐

strides in Pooling Layers

import tensorflow as tf
 
from tensorflow.keras.layers import MaxPooling2D
 
images = tf.random.normal(shape=(1, 28, 28, 3))
pool = MaxPooling2D(pool_size = 3, strides =2)
y = pool(images)
 
# n_H_ = [(n_H + 2p - f)/s + 1]
print(images.shape)
print(y.shape)

I/O Shapes

$n_{H}^{'}=\left[ \dfrac{n_{H}+2p-f}{s}+1\right] $

이 식은 conv,pooling 모두 적용가능함

---

참고 및 출처 : https://koreapy.tistory.com/603 , https://medium.com/machine-learning-algorithms/what-is-padding-in-convolutional-neural-network-c120077469cc ,